MAPPING

Mapped space is an index into another representation or between representations. It is used to relate systems without intrinsic common referents. An example of mapping is that of the city street map. In trying to find the street for a given name, the map is usually set up in a coordinate system. Given a street name, one can find the coordinates. Then the search for the street is limited to one cell in the grid.

There are two types of mapping, direct-mapping and mediated mapping. The city map is an example of indirect mapping. Mediated mapping points toward an area, but some search is still required.

Direct mapping allows a specific component to be obtained with no search. In application of direct mapping, the scale of the interval is determined by the smallest component. The range is determined by the proportion of the smallest entity to the largest.

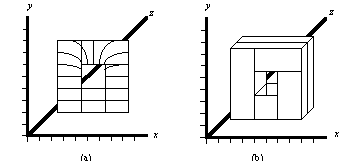
Figure 83 illustrates a mediated mapping, where a cartesian coordinate system allows a mapping between two dissimilar systems. Generally, the results of a finite-element analysis can be made available for automated analysis. Some systems provide evaluation data and x-y coordinates in the form of a text file. In this example, let it be supposed that the flow analysis of Figure 83 (a) indicates a welding line at the top, and a consequent structural weakness at that point. Ideally, this information can be used in conjunction with some other analysis. Yet it has to be referred to within the context of the solid model of Figure 83 (b). The coordinate system allows an indexing and indirect correspondence of the "features" of the flow simulation with areas or features, such as the hole, of the geometric model.

Coordinate mapping is a viable, intermediate mapping for engineering systems. A set of general systems could use the coordinate system to index to other systems in lieu of direct mapping. Mapping is important for integrating the results from a variety of applications. Coordinates are the only thing that can be agreed to, although the point of origin and units of measurement may cause problems if not conveyed accurately.

Figure 83 Example of Mediated Mapping. (a) Flow Analysis and (b) Solid Model. Both involve shared convention of coordinated index of (a) and (b).

For integration of disparate systems around an artifact, there must be a coordinating model available, like the shared convention of language. Abstraction does not allow for reference back to the original representation. Derivation makes for a tightly coupled system, for instance between a geometric model to a FEM mesh analysis back to the original model. But such integration lacks the openness available through mapping via a third, common coordinate system. Many systems, however, lack even this basic concept of coordinated mapping, so that the results of applications from one vendors cannot be used as input to another vendor's application.